こんにちは！
今回は、楽譜の音程判断の応用編として、「転回音程」の仕組みについて解説していきます！
これまでの記事で音程の基本的な数え方や種類は見分けられるようになったけど、「転回音程って何だか難しそう…」と感じている方もいるかもしれません。
しかし、転回音程は決して難しい考え方ではなく、基本ルールさえ押さえれば、簡単に理解できます！
また、転回音程を知ることは、次のようなメリットがあります！
- 和音の理解が深まる（和音の転回形に繋がる！）
- メロディーの関連性や音楽の構造が見えやすくなる
- 音楽理論の面白い側面を発見できる！
この記事では、次の内容を知ることができます！
- 転回音程の基本的な作り方とその定義
- 転回すると度数と種類がどう変わるかの法則
- 転回音程を学ぶメリットと音楽的な活用ヒント
今回の内容は、これまでの記事で解説した音程の基本的な知識が前提となります。
まだの方は、ぜひそちらを先にご覧ください！
転回音程が分かると、音楽の「裏側」が見えてきて、さらに音楽の面白さが深まります！
一緒に楽しく学んでいきましょう！
参考にしている書籍はこちら！
転回音程の作り方：基本ルールと手順をマスター！
では、具体的に転回音程はどうやって作るのでしょうか？
その基本ルールと手順を見ていきましょう。
転回音程の定義：2つの音のうち、一方の音を1オクターブ上または下に移動させる。
転回音程とは、2つの音でできている音程のうち、どちらか一方の音を1オクターブ動かして作る新しい音程のことです。
転回音程を作る方法としては、次の2パターンがあります。
- 低い方の音を1オクターブ上げる。
- 高い方の音を1オクターブ下げる。
どちらの方法を使っても、結果として出来上がる転回音程は同じになります。
やりやすい方で考えてみましょう。
譜例で見てみよう！転回音程のビフォーアフター
実際の譜例で見てみましょう！
譜例
この音程を転回させてみましょう！
・方法1：低い方の音「ファ」を1オクターブ上げる。
→「ド（C5）」と「1オクターブ上のファ（F5）」の音程になります。
・方法2：高い方の音「ド」を1オクターブ下げる。
・すると、「1オクターブ下のド（C4）」と「ファ（F4）」の音程になりますが、通常は低い方の音を基準に考えるので、これも「ド」と「ファ」の関係として捉えます。
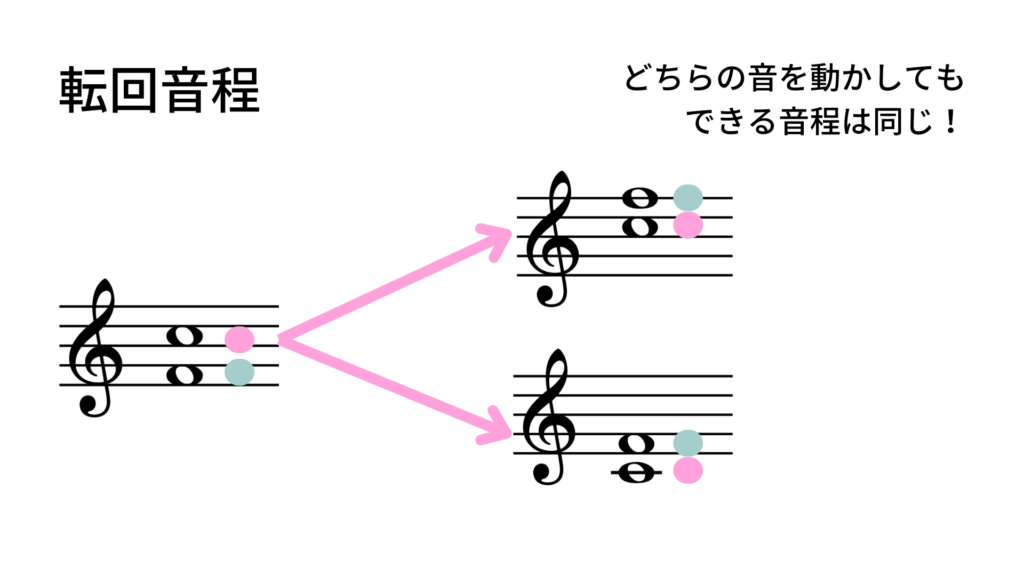
どちらの方法でも、結果として「ド」と「ファ」という音の組み合わせの音程ができることが分かると思います！
このように、元の音程の音をオクターブ移動させることで、全く別の音程が生まれます！
転回するとどう変わる？度数と種類の変化には法則がある！
転回音程を作ると、元の音程と比べて「度数」と「種類」が変化します。
「度数」と「種類」が変化に関する「法則」を紹介します！
転回音程の「度数」の変化 ～足して「9」の法則～
まず、度数がどう変わるか見てみましょう！
度数の変化は、元の音程の度数と、その転回音程の度数を足すと、必ず「9」になります！
具体的に確認してみましょう！
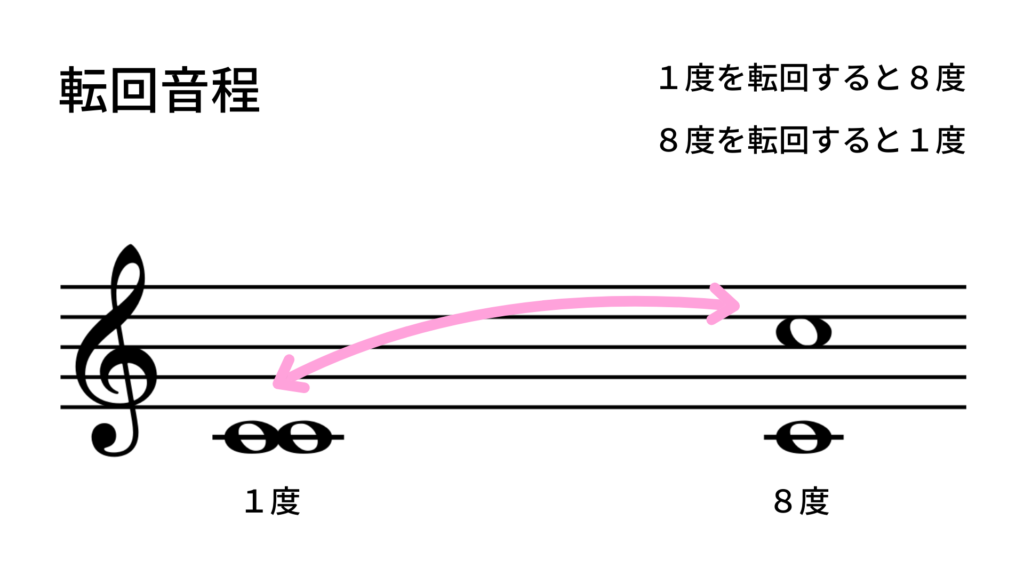
・1度は転回すると8度（1 + 8 = 9）
・2度は転回すると7度（2 + 7 = 9）
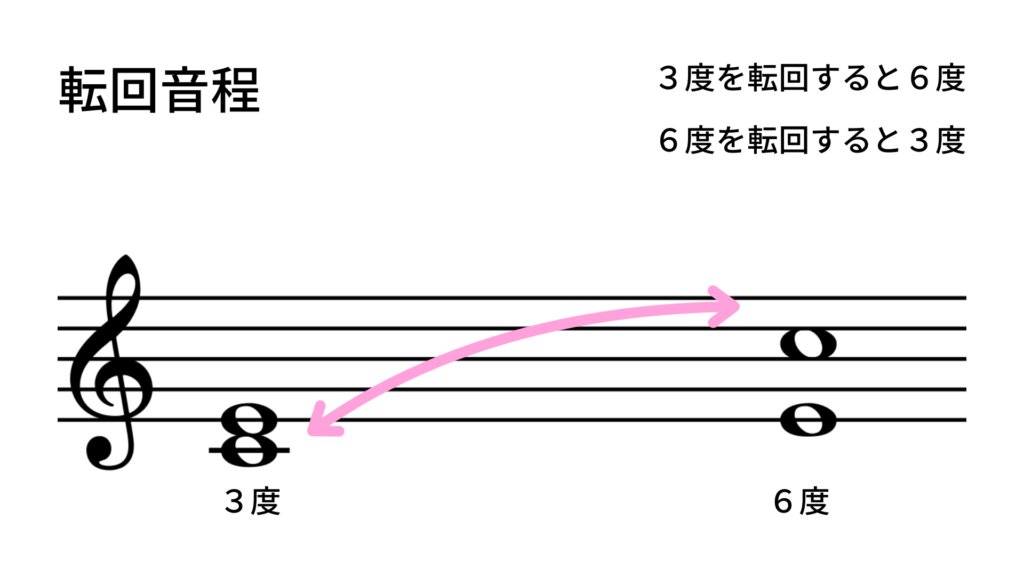
・3度は転回すると6度（3 + 6 = 9）
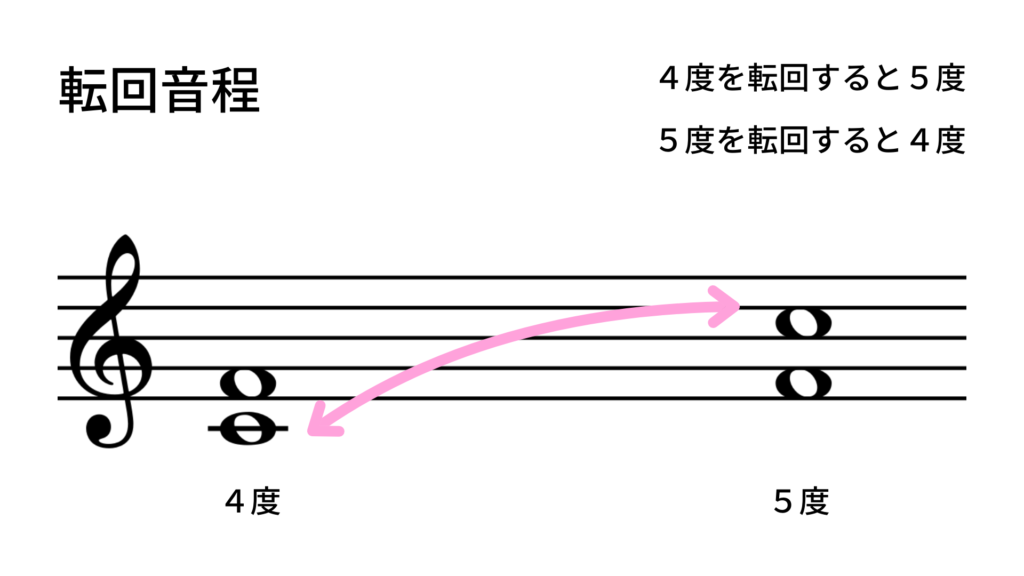
・4度は転回すると5度（4 + 5 = 9）
・5度は転回すると4度（5 + 4 = 9）
・6度は転回すると3度（6 + 3 = 9）
・7度は転回すると2度（7 + 2 = 9）
・8度は転回すると1度（8 + 1 = 9）
この法則を使えば、元の音程の度数が分かれば、その音程を転回した後の度数はすぐに計算できます！
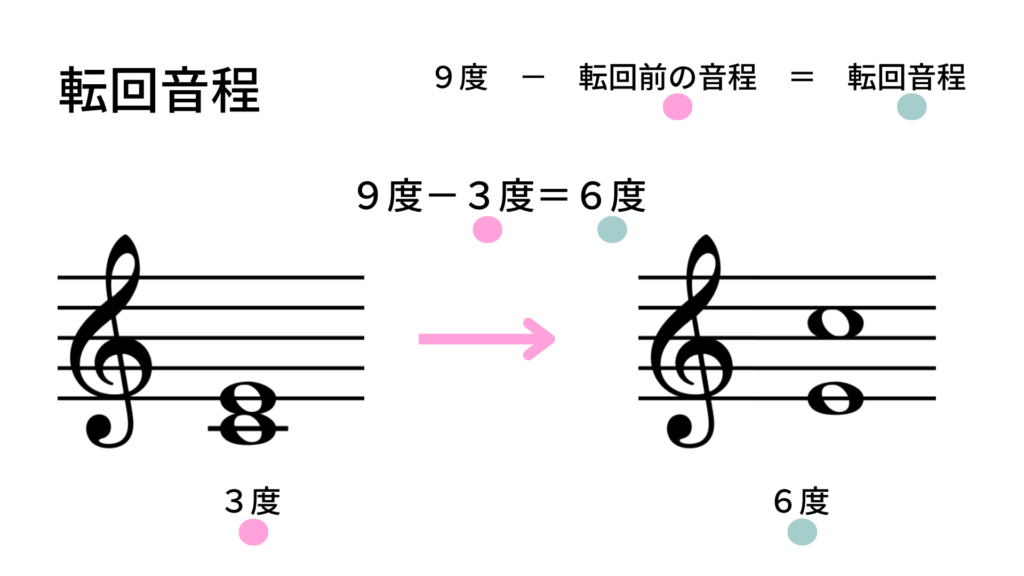
例えば、元の音程が3度なら、転回音程は「9 – 3 = 6度」となるわけです。
転回音程の「種類」の変化 ～ペアで覚える変化パターン～
次に、音程の種類（完全、長、短、増、減）がどう変わるかを紹介します！
これも、決まった変化のパターンがあります！
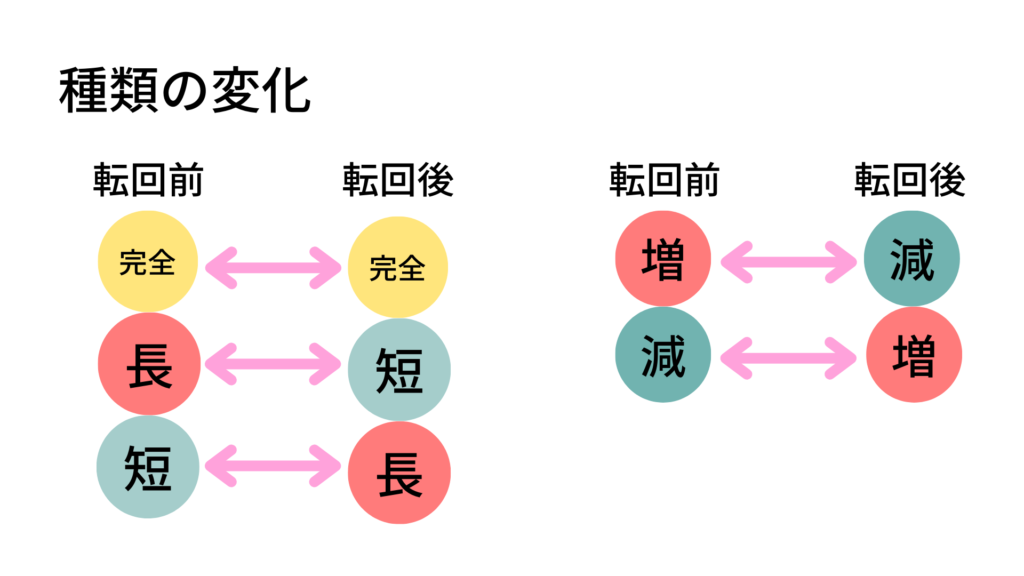
覚えておくべき変化のペアは次の通りです。
- 完全音程 ⇔ 完全音程
- 長音程⇔ 短音程
- 増音程 ⇔ 減音程
つまり、転回音程の種類は、次のように知ることができます！
- 「完全」音程を転回すると、種類は「完全」のまま。
- 「長」音程を転回すると、種類は「短」に変わる。
- 「短」音程を転回すると、種類は「長」に変わる。
- 「増」音程を転回すると、種類は「減」に変わる。
- 「減」音程を転回すると、種類は「増」に変わる。
このペア関係を覚えてしまえば、種類がどう変化するかも簡単に分かりますね！
譜例で確認！元の音程と転回音程の具体的な変化
では、実際にいくつかの音程を転回させて、度数と種類がどのように変化するのかを見てみましょう！
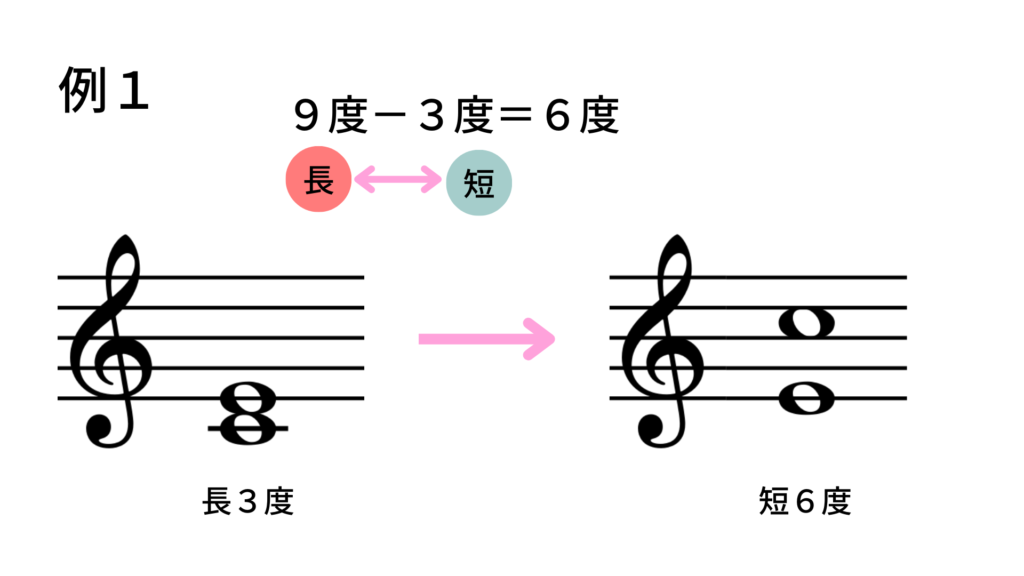
度数：「3度」 → 転回すると 9 – 3 = 「6度」
種類：「長」 → 転回すると 「短」
結果：転回音程は「短6度」（ミと1オクターブ上のド）
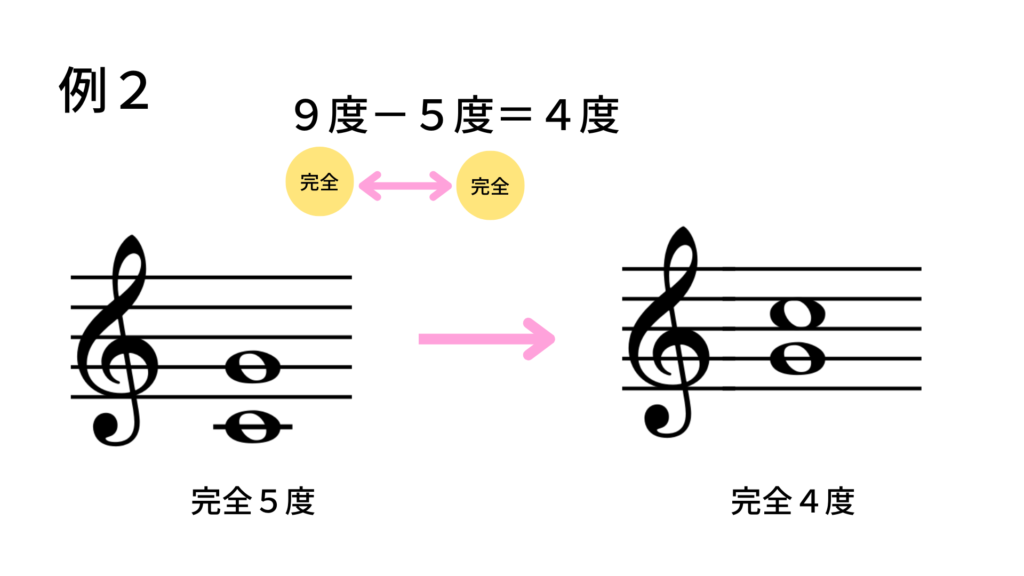
度数：「5度」→ 転回すると 9 – 5 = 「4度」
種類：「完全」 → 転回すると「完全」
結果：転回音程は「完全4度」（ソと1オクターブ上のド）
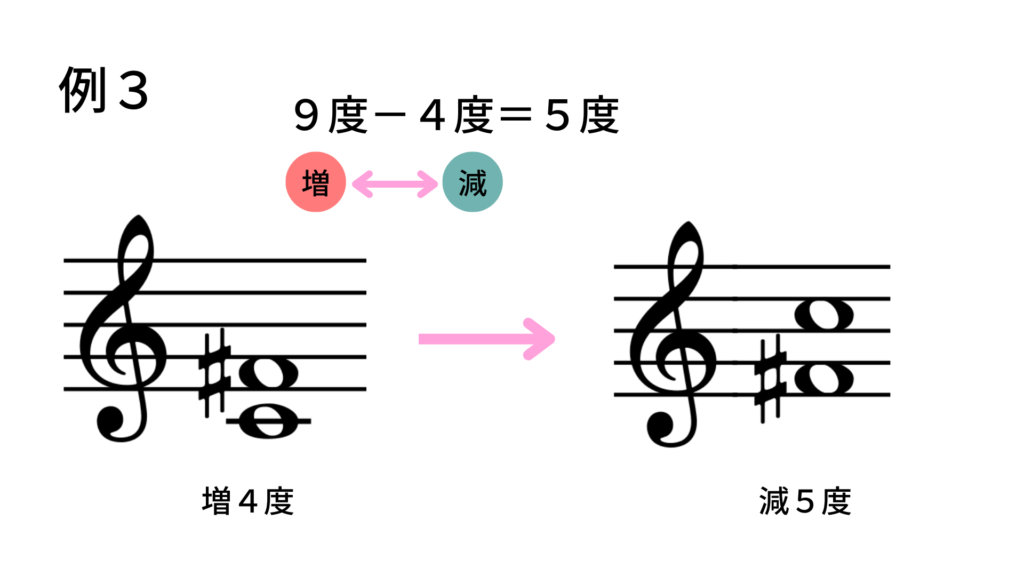
度数：「4度」 → 転回すると 9 – 4 = 「5度」
種類：「増」 → 転回すると 「減」
・結果：転回音程は「減5度」（ファ♯と1オクターブ上のド）
このように、2つの法則「度数は足して9」「種類はペアで変化」を使えば、どんな音程でもその転回音程を導き出すことができます！
実践！転回音程の判断トレーニング
法則が分かったら、次は実際に練習してみましょう！
練習問題：元の音程から転回音程を導き出してみよう！
以前の記事で出てきた練習問題の音程を、今度は転回させてみましょう！
譜例５は、単音程に直してから考えてみてください！
元の音程の度数と種類をまず判断し、そこから転回音程の度数と種類を答えてください。
最初は少し時間がかかるかもしれませんが、法則を意識しながら繰り返し練習することで、だんだんスムーズに判断できるようになります！
以下の解答を確認して、答え合わせをしましょう！
・譜例1の元の音程：増1度 (ソとソ♯)
・転回音程の度数：9 – 1 = 8度
・転回音程の種類：増 ⇔ 減 なので、減8度
・答え：減8度 (ソ♯と1オクターブ上のソ)
・譜例2の元の音程：短3度 (ミとソ)
・転回音程の度数：9 – 3 = 6度
・転回音程の種類：短 ⇔ 長 なので、長6度
・答え：長6度 (ソと1オクターブ上のミ)
・譜例3の元の音程：完全4度 (ファとシ♭)
・転回音程の度数：9 – 4 = 5度
・転回音程の種類：完全 ⇔ 完全 なので、完全5度
・答え：完全5度 (シ♭と1オクターブ上のファ)
・譜例4の元の音程：短6度 (レとシ♭)
・転回音程の度数：9 – 6 = 3度
・転回音程の種類：短 ⇔ 長 なので、長3度
・答え：長3度 (シ♭と1オクターブ上のレ)
・譜例5の元の音程：増9度 (ドと1オクターブと少し上のレ♯)
・まず単音程に直す。→増2度。
・転回音程の度数：9 – 2 = 7度
・転回音程の種類：増 ⇔ 減 なので、減7度
・答え：減7度 (レ♯と1オクターブ上のド)
転回音程は何の役に立つの？音楽の中での活かし方（ヒント）
さて、転回音程の作り方や法則は分かりましたが、これが実際に音楽の中でどんな風に役立つのでしょうか？
転回音程を役に立たせるヒントを紹介します！
和音の理解がもっと深まる！～和音の転回形への第一歩～
皆さんがよく知っている「ドミソ」の和音を例に考えてみましょう！
一番下に「ド」の音がある場合と、「ミ」の音がある場合、または「ソ」の音がある場合では、同じ「ドミソ」の構成音でも響きの印象が少し変わります！
これは「和音の転回形」といって、和音の一番下の音（バス）が変わることで、和音全体の響きや機能が変化する現象です。
この和音の転回形を理解する上で、転回音程の考え方は非常に重要な基礎になります。
例えば、「ドミソ」の和音では、ドとミは長3度、ドとソは完全5度ですが、ミが一番下に来る「ミソド」の形では、ミとソは短3度、ミとド（上の）は完全4度となります。
このように、転回音程では、構成音間の音程関係が変わってきます。
今回は和音の転回形の詳細に紹介しませんが、転回音程が和音の理解に繋がる第一歩だということを覚えておくといいですね！
メロディーやハーモニーの「隠れた関係」が見えてくる！
時には、あるメロディーラインと、それに対して付けられた別のメロディーライン（対旋律、カウンターメロディーなど）が、実は転回音程の関係になっていることがあります。
例えば、主旋律が「ド→ミ」と上がっているのに対し、対旋律が「ミ→ド（下の）」と下がっている場合、音の動きは逆ですが、音程の度数や種類には関連性が見られることがあります。
転回音程の知識があると、こうした音楽の中の「隠れた構造」や「音の繋がり」に気づきやすくなり、曲の分析がより面白くなります！
音楽の「裏側」を知る面白さ、分析の楽しさ
転回音程を理解するということは、作曲家がどのように音を巧みに組み合わせ、響きを変化させ、音楽に彩りを与えているのか、その意図や工夫の一端を垣間見るようなものです！
「この音程を転回させると、こんな響きになるのか！」という発見は、まるで音楽のパズルを解いているような楽しさがあります！
音程という視点から音楽の「裏側」を少し覗いてみることで、普段聴いている音楽も、また違った角度から楽しむことができるようになるかもしれません！
まとめ
いかがでしたか！
今回の記事では、転回音程の基本的な仕組みと、その度数や種類がどのように変化するかの法則について解説しました！
- 転回音程とは、2つの音のうち一方を1オクターブ動かして作る新しい音程であること。
- 転回すると、元の音程と度数を足して「9」になり、種類は「完全⇔完全」「長⇔短」「増⇔減」のペアで変化する法則があること。
- 転回音程の知識は、和音の理解や音楽分析など、より深い音楽学習に繋がること。
転回音程の判断は、音楽をより深く、そして論理的に理解するための重要なステップです！
これからの演奏に役立ててください！
その他の記事も、是非ご覧ください！
基礎練習と並行しながら、様々な曲の練習をするのもオススメです！
以下のページで販売しているので、ご活用ください！
